このポイント集で筆記試験合格を目指しましょう。毎年、最新情報で皆さんをバックアップします。
第1章 電気回路の問題
■ポイント・・・・ここで覚えて頂きたいポイントは以下の通りです。
1.オームの法則

左の図では、電池V[V]に抵抗R[Ω]をつないでいます。
この回路で、電池の電圧Vを大きくすると、回路に流れる電流は大ききくなります。また、電圧は一定として抵抗Rの値を小さくすると、回路に流れる電流は大きくなります。
つまり、回路の電流I[A]は、電圧の大きさに比例し、抵抗の大きさに反比例することがわかります。この関係から以下の式が導き出せます。
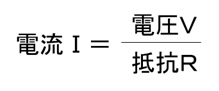
 この形で覚えておく
この形で覚えておく
(VはI×R、IはV/R、RはV/I)
これがオームの法則です。
2.消費電力
消費電力とは、回路で使用し消費される電力です。電力P=電流I×電圧V[W:ワット]で求まります。前述のオームの法則の式から以下のように変形することができます。
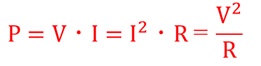
3.発熱量の求め方
発熱量H=電圧V×電流I×時間t [J:ジュール]
※電力量も同じ式で算出できます。ただし電力量の単位は[ws]です。
すなわち1J=1Wsということです
4.抵抗の合成抵抗
抵抗を直列に接続した場合や、並列に接続した場合の合成抵抗を求める方法です。
(1)直列接続の場合
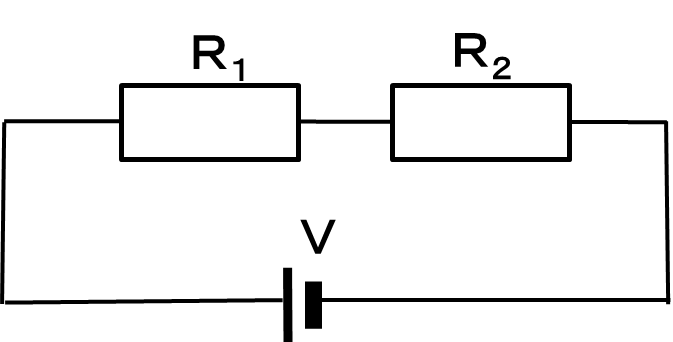
直列に接続した場合は、単純に合計すれば求まります。
左図のような回路の場合、合成抵抗R0=R1+R2
(2)並列接続の場合
5.合成抵抗の求め方
抵抗を直列に接続した場合や、並列に接続した場合の合成抵抗を求める方法です。
(1)直列接続の場合

直列に接続した場合は、単純に合計すれば求まります。
左図のような回路の場合、合成抵抗R0=R1+R2
(2)並列接続の場合
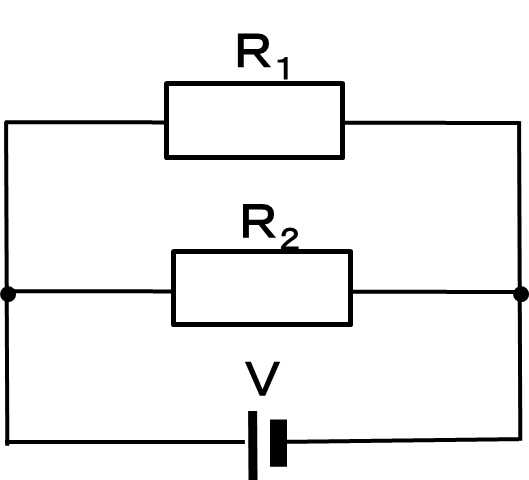
並列接続の場合は、以下の式で求めます。
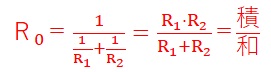
5.導線の抵抗
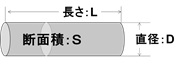
下図のような導線(長さL[m]、断面積S[m2]、直径D[m])の抵抗を求める式
※導体の抵抗は、長い程大きくなりますよね。また断面積が大きい程電子が動きやすくなるので、抵抗は小さくなります。このことから、導線の抵抗は以下の式で表わされます。
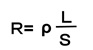 ρ:抵抗率で、ロウと読みます。単位は[Ω・m]です。
ρ:抵抗率で、ロウと読みます。単位は[Ω・m]です。
この式を変形する問題が出ています。断面積S=半径×半径×π=(D/2)2×πを代入すると、
次の式になります。さらに、この式を抵抗率ρ=に変換する問題も出ています。
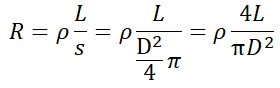
式の変換が得意な人は覚えておきましょう。
また、導線の長さや断面積の大きさにより抵抗値を比較する問題が出ています。
このような問題では計算をしていては、大変なので、以下のように図で概念的に理解します。

①最上段の抵抗をR1とします。
②長さが2倍(2L)になれば、抵抗R2は2倍になります。
③長さが同じLでも、直径Dが2倍になると
抵抗はDの2乗に反比例するので、抵抗R3はR1の1/4になります。
| ■■過去問■■ 過去問は動画で説明しています。こちらでご覧ください。 【1】a-b間の電圧を求める問題 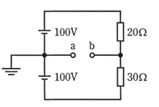 ①まず、回路に流れる電流を求めます。 電池の合計電圧は200V、抵抗は50Ωになりますので、I=200V/50Ω=4[A] ②次に30Ωの抵抗の両端電圧=4A×30Ω=120V ③従って、a点は100V、b点は120Vになりますのでa-b間の電位差は120-100V=20Vとなります。 【2】SWを閉じたときのa-b間の電圧を求める問題 左図の回路でSW(s)を閉じたときのa-b間の電圧を求める問題です。  ①Sを閉じると、その下にある抵抗50Ωには、電流が流れず、全SW側に流れます。 (SW側は抵抗が0だから) ②またa、b端子はつながっていませんので、電流は流れていませんので、その右側にある抵抗50Ωもない のと同じです。 ③従って、回路を流れる電流Iは、 I=120V/100Ω=1.2Aとなります。 ④よって、50Ωの両端電圧(a-b間)Vは、 V=1.2A×50Ω=60Vで求まります。 【3】回路(a-b間)の合成抵抗を求める問題 下図のような回路の合成抵抗を求める問題です。 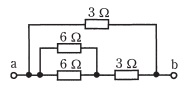 ①6Ωと6Ωの並列回路から求めていきます。並列なので合成抵抗=積/和=6*6/(6+6)=3〔Ω〕 ・・・同じ抵抗値で並列の場合は、元の抵抗の半分でしたね。 ②次に3Ω+3Ω=6Ωの抵抗と、一番上の3Ωの並列になるので、同様に 合成抵抗= 積/和=6*3/(6+3)=18/9=2〔Ω〕 になります。 【4】電流計Aの指示が1[A]のとき、電圧計Vの指示は? 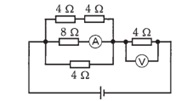 ①8Ωに1A流れているので両端電圧は8Ω×1A=8Vとなる。 ⇒ポイント:並列回路の場合、両端電圧はどこも同じである。 ②4Ω+4Ωの回路に流れる電流は、電圧は8Vなので、8V/8Ω=1A ③4Ωを流れる電流は、同様に、8V/4Ω=2A ④従って、回路全体を流れる電流は1A+1A+2A=4A ⑤右側の4Ωの抵抗には4[A]流れているが分かったので、両端電圧は4Ω×4A= 16〔V〕となる。 【5】抵抗Rで消費する電力を求める問題  (考え方)まずは、前述2項に示した消費電力を求める式を書いてみましょう。この問題の場合、回路に流れる電流は10[A]となっています。また抵抗Rの大きさはわからないので、P=V・Iの式で求まりそうです。 このとき電源電圧は100[V]となっていますので、10Ωと40Ωの並列箇所の電圧が求まれば、抵抗Rの電圧が求まります。 ① 10Ωと40Ωの並列回路の合成抵抗=(10*40)/(10+40)=400/50=8[Ω] ②従って、この並列回路の電圧V=10[A]× 8[Ω] =80[V] ③以上により、抵抗Rの電圧は20[V]、流れる電流は10[A]ですので、 P= V・I =20×10=200[W] 【6】電線の接続不良で接続点の接触抵抗が0.5Ωとなった。この電線に20A流れると接続点から1時間に発生する熱量〔kJ〕は? ①発熱量H=V・I・t=I2・R・t[J]で求まります。また、1[J]=1[Ws]です ②I=20A、抵抗が0.5Ωなので、1時間を秒に変換して計算すれば良いですね。 ③ H=I2・R・t=(20)2×0.5×(60分×60秒) =400×0.5×3600=720000[J] =720[kJ] 【7】直径2.6mm、長さ10mの銅導線と抵抗値が最も近い同材質の銅導線は。 イ: 直径1.6mm、長さ20m ロ: 断面積5.5㎟、長さ10m ハ: 直径3.2mm、長さ5m 二: 断面積8㎟、長さ10m ①この問題の場合は、計算する必要はありません。 長さが同じで、断面積が近いものを選びます。 ②そうすると、2.6mmの場合の断面積S≒5.3㎟なので、一番近いのは、ロになります。 2.6mm=5.5㎟と覚えておくと、即、回答できます。 |


